Auflösungverlust durch mehrfache DA-Wandlung?

Bei nichtperiodischen Signalen behandelt man die wie ein periodisches Signal mit unendlicher Länge.
In der Praxis ist die eine Perioden endlich lang. Irgendwann ist die Mucke aus.

ZeeeM (Beitrag #52) schrieb:

Bei nichtperiodischen Signalen behandelt man die wie ein periodisches Signal mit unendlicher Länge. In der Praxis ist die eine Perioden endlich lang. Irgendwann ist die Mucke aus. :D

Verstehe den Zusammenhang zur Bittiefe nicht, sorry.

Hat mit Bittiefe nicht zu tun.
Für den Hörsinn ist Bittiefe Störabstand.
Die Frage ist eigentlich, wie viel Information kann man weglassen, bevor das wirklich signifikant nachzuweisen ist.
Interessant ist dabei im Vergleich zu analogen Verlusten.
Man bemüht sich mit hochgenauen Taktgeber, um klanglich mehr zu bekommen, spielt aber mit Begeisterung Schallplatten ab,
Da soll man nicht ins Grübeln kommen?

Ich denke man hört Platten, weil die Masterings da häufig die "besseren" sind, sehr oft mit deutlich mehr Dynamik. Das klingt dann durchaus besser (insb. wenn man die Aufnahmen digitalisiert und dann "restauriert").

Tobiii2 (Beitrag #55) schrieb:

Ich denke man hört Platten, weil die Masterings da häufig die "besseren" sind, sehr oft mit deutlich mehr Dynamik. Das klingt dann durchaus besser (insb. wenn man die Aufnahmen digitalisiert und dann "restauriert").

Das sind aber Alles keine Aspekte des Transportmediums, zumal Digital vom physischen Träger entkoppelt.
Viel geht durcheinander, da man subjektive Eindrücke mit technischen Eigenschaften vermischt und obendrein macht man sich das noch zwecks Geldernte zunutze,

Der Witz an einem bandbreitenbegrenzen Signal ist es ja, das man es mit einer endlichen Anzahl von Summanden einer Fourierreihe darstellen kann.

Es gibt in der Audiosignal Realität leider kein völlig Bandbreiten begrenztes Signal. (Filter Beschränkungen)
Die Annahme eines 100% Bandbreiten begrenzten Signal um dem Shannon / Nyqusit Abtasttheorem zu entsprechen und eine
theoretisch fehlerfreie Interpolation/Rekonstuktion zu ergeben ist nicht erfüllt.
Es gibt eben doch Rekonstruktionsfehler entsprechend dem getriebenem Aufwand.

Und diese Fehler hört man halt, oder nicht

ZeeeM (Beitrag #56) schrieb:

Viel geht durcheinander, da man subjektive Eindrücke mit technischen Eigenschaften vermischt ...

Das kommt auch davon, wenn man die Leute so in die Ecke drängt, wie das hier im Forum z.B. gerne geschieht. Denn dann bleibt den Leuten am Ende auch nichts Anderes übrig, als irgendeine technische Überlegenheit der Platte zu suchen. Und da bleiben dann ja nur Dinge wie Jitter oder eben die "Auflösung" ("Treppenstufen") übrig.

Manchmal mag man ja auch einfach gewisse Unzulänglichkeiten (Verzerrungen, etc.). Bei meiner Oma brannten Pfannkuchen immer an ein paar Stellen ein bisschen an. Ich habe mir extra eine Stahlpfanne gekauft, damit ich das auch hinbekomme, nicht-angebrannt schmecken sie mir einfach nicht so gut

frank60 (Beitrag #43) schrieb:

Burkie (Beitrag #10) schrieb: die Bezeichnung "Auflösung" ist etwas missdeutig und fehlleitend. Die Bit-Auflösung bestimmt den Signal-Rauschabstand, fertig. Mehr nicht. Keine "feinen Details", nix. Was natürlich nicht stimmt. Selbstverständlich steigt die Auflösung.

Der einzige Effekt einer erhöhten "Auflösung" ist lediglich ein größerer Signal-Rauschabstand, mehr nicht. Wirklich nicht.

Grüße

Anro1 (Beitrag #57) schrieb:

Der Witz an einem bandbreitenbegrenzen Signal ist es ja, das man es mit einer endlichen Anzahl von Summanden einer Fourierreihe darstellen kann. Es gibt in der Audiosignal Realität leider kein völlig Bandbreiten begrenztes Signal. (Filter Beschränkungen)

Doch, die gibt es.
Dort im Spektrum zu den hohen Tönen hin, bei dem die Schmerzgrenze mit der Wahrnehmungsgrenze zusammenfällt, ist Ende Gelände fürs menschliche Gehör.
Damit man also gewisse sehr hohe Töne überhaupt noch wahrnimmt, müssten sie so laut sein, dass es im Ohr schon wieder schmerzen würde. Das ist also die Grenze des Gehörs.

Nun will man also nur solche Töne, solche Tonhöhen noch digitalisieren, die zwar noch (gerade so) wahrnehmbar sind, aber im Ohr noch nicht schmerzen.
Digitalisieren heißt, mit eine endlichen "Auflösung", Bit-Anzahl und somit Signal-Rauschabstand zu digitalisieren.

Sagen wir mal, es seien 16 Bit und somit (auch in den höchsten Höhen) ca. 96 dB Rauschabstand (bei Vollaussteuerung).

Dann genügt es, wenn das Bandpass-Filter kurz vor Nyquist-Frequenz mit ca. 96 dB Dämpfung sperrt.
Für die A-D-Wandlung ist das so gut wie "völlig gesperrt, völlig bandbreiten-begrenzt".

Grüße

Ingor (Beitrag #35) schrieb:

Samplingrate und Bittiefe können gegeneinander ausgetauscht werden, Das macht sich der sog. Deltawandler zu nutze, der nur zwischen 0 und 1 schaltet. Durch eine entsprechend hohe Samplingrate erreicht man damit aberz.B. die Qualität eines 16 Bit Wandlers.

Das ist ein anderes Codierungsverfahren mit entsprechender Überabtastung. Ich sehe da keinen Zusammenhang zu der Aussage, die ja sogar einen gegenteiligen Zusammenhang suggeriert ("dass zu einer solchen Samplingtiefe auch eine entsprechende Samplingfrequenz sinnvoll ist").

Burkie (Beitrag #36) schrieb:

Die Bit-Auflösung bestimmt den Signal-Rauschabstand, fertig. Mehr macht sie nicht, insbesondere keine "Feindynamik" oder ähnliche Phantome.

Wie gesagt, technisch richtig, aber der Begriff suggeriert etwas anderes, weil da eben der Quantisierungsfehler als "Rauschen" bezeichnet wird - es ist aber kein Rauschen, wie man sich das als normaler Mensch vorstellt. "Feindynamik" ist ja ein überhaupt nicht definierter Begriff aus dem Schwurbelwörterbuch der Gazetten klingt toll, kann aber alles möglich sein, genau wie "Auflösung". Je nachdem, was man darunter versteht, könnte man eine Verringerung des Quantisierungsfehlers auch als verbesserte "Feindynamik" verstehen.

sealpin (Beitrag #44) schrieb:

Auch mit 8Bit kann ich 20khz perfekt digitalisieren und auch wieder zurückwandeln. Da fehlt nichts, einfach weil die Vorstellung, dass die Bit Anzahl irgendwas mit der genaueren Abtastung eines Audiosignals zu tun hat (es gibt keine Treppenstufen ...) falsch ist.

Nein, die ist nicht falsch. Korrekt, es gibt keine Treppenstufen, aber dennoch entsteht wegen der diskreten digitalen Werte ein Quantisierungsfehler, der dafür die "Perfektion" reduziert. Hier am Beispiel von 4 Bit zu sehen: https://upload.wikimedia.org/wikipedia/commons/b/bf/Pcm.svg

Auch wenn das zurückgewandelte Signal glatt ist, es ist nicht perfekt. Es ist halt nur bei 16 Bit bereits so gut, dass eine weitere Verbesserung einfach nicht mehr hörbar ist.

flexiJazzfan (Beitrag #48) schrieb:

Die Vorstellung, man habe jetzt die perfekte Übermittlung dieses komplexen Geschehens livehaftig in jedes Wohnzimmer endlich gelöst, hält sich seit Jahrzehnten. (...) Ich bin noch nicht dafür, die Grenzen der Musikreproduktion als erreicht zu bezeichnen.

Die Realisierung dieser Vorstellung scheitert aber nicht an unzureichender Signalverarbeitung, sondern den Grenzen der Stereophonie, Raumakustik, Lautsprecher, Aufnahmetechnik, ... Was die Signalverarbeitung einschließlich ihrer Konservierung angeht, haben wir praktisch Perfektion. Die Baustellen sind ganz woanders, und da muss man schon bei den Aufnahmen anfangen.

Die ingenieursmäßige Betrachtungsweise: "Das reicht so weit völlig aus" hat uns ja schon MP3 beschert und die verschiedenen unsäglichen komprimierten Bilddarstellungsformate (8 Bit Farbtiefe).

Man muss eben unterscheiden zwischen den Verschlechterungen, die noch im Bereich des Wahrnehmbaren liegen, und denen, die einfach zu gering sind, um unsere Wahrnehmung noch zu beeinflussen. Letztere sind für mich perfekt - die Suche nach noch weiterer Verbesserung mag man zwar anstreben, wenn einem das Befriedigung verschafft, aber das hat dann nichts mehr mit Musikgenuss zu tun.

Anro1 (Beitrag #57) schrieb:

Es gibt in der Audiosignal Realität leider kein völlig Bandbreiten begrenztes Signal.

Wovon sprichst du, vom originalen Schallereignis, das man aufnehmen möchte? Bei der späteren Verarbeitung gibt es natürlich ein bandbreitenbegrenztes Signal, spätestens bei der Digitalisierung.

Dadof3 (Beitrag #62) schrieb:

Burkie (Beitrag #36) schrieb: Die Bit-Auflösung bestimmt den Signal-Rauschabstand, fertig. Mehr macht sie nicht, insbesondere keine "Feindynamik" oder ähnliche Phantome. Wie gesagt, technisch richtig, aber der Begriff suggeriert etwas anderes, weil da eben der Quantisierungsfehler als "Rauschen" bezeichnet wird - es ist aber kein Rauschen, wie man sich das als normaler Mensch vorstellt.

Heutzutage wird mit aktuellen Wandlern so gewandelt, dass es tatsächlich ein echtes zufälliges Rauschen ist - fertig.
Der Quantisierungsfehler, die Quantisierungs-Rundungsfehler sind bei aktuellen Wandlern ein echtes Rauschen, und keine Verzerrungen mehr. Dank Dithering und Noise-Shaping.
Bei 16 Bit "Auflösung" ist dieser Unterschied allerdings eh nur akademischer Natur.
Mit 16 Bit gewandelt, klingen die Quantisierungsverzerrungen bei vernünftigen Abhör-Lautstärken eh nur wie Rauschen - wenn man sie denn überhaupt hören kann! Denn dazu müsste man die Anlage auf ca. 120 dB (eher sogar noch etwas mehr) Schalldruckpegel bei digitaler Vollausteuerung (0 dBFS) aufdrehen.

"Feindynamik" ist ja ein überhaupt nicht definierter Begriff aus dem Schwurbelwörterbuch der Gazetten klingt toll, kann aber alles möglich sein,

Und deshalb eignet er sich ja so gut, um Leuten, die sich mit den Grundlagen der Technik nicht wirklich auskennen, allen Quark verkaufen zu können.

Grüße

Ich bleibe dabei es gibt bei der Musikaufnahme die beiden Größen : Größe Druckamplitude und zeitliche Abfolge der Änderungen. Beides wird von den Musikern aufs feinste moduliert und variiert (und natürlich auch gehört). Für die Aufnahme , Weiterleitung und Konservierung dieser Größen erwarte ich von der Technik die bestmögliche Lösung. Die Größenordnungen sind klar. Es geht um immer um mehrere Zehnerpotenzen: Schallldruck von 2 Mikropascal bis 2 Pascal (100 dB) und Frequenzen von 20 - 20 Tausend Herz.
Die Frage, ob meine Anlage mit ihrem Analogteil oder meine Lautsprecher den Aufwand der Ton- und Informationstechniker auch wirklich würdigen können oder ob meine alten Ohren das alles noch so mitbekommen ist verdammt noch mal nicht Problem der Digitalelektroniker! Da arbeiten schon noch andere dran und haben noch jede Menge zu tun - auch bei den Mikrofonen!
Wer jetzt meint, man dürfe zarte Lautstärkeunterschiede in Musikmaterial nicht Feindynamik nennen, (weil er eh nur Metal hört?) , der soll einen anderen Begriff einführen. Es gibt da aus der Akustik schon die exakten physikalischen definierten Bezeichnungen, welche das Thema der kleinen Lautstärkeabstufungen aber auch nur in Energie- Kraft- oder Bewegungstermen darstellt und es nicht mit dem informationstechnischen Begriff des Rauschens vermengt.
Ein Beispiel für musikalische "Kleinsignale" : Ein lang anhaltender Trompetenton zeigt in der Druckamplitudendarstellung eine Sinusschwingung . Diese ist leicht moduliert , "verwellt" , durch eine Menge regelmäßiger kleiner Obertonschwingungen und noch kleinerer Partialschwingungen des Trompetenmetalls, darauf "sitzen" noch kleinere gänzlich unregelmäßige Spitzen. Diese rühren vom "Spratzen" der Feuchtigkeit in der Trompete und von der Rauhigkeit der Tonerzeugung durch die Lippen her. Unabhängig vom gespielten Ton kann man an diesen winzigen Effekten den individuellen Klang einer Trompete und die spezielle Spielweise des Trompeters (z.B. Klassik oder Jazz) erhören und erkennen.

Die Entscheidung, was ich davon noch hören sollte und was nicht, kann meinetwegen der Tontechniker bei der Abmischung entscheiden aber nicht die Informationstechniker und Elektroingenieure deshalb : Highest Resolution !!!

Gruß Rainer

flexiJazzfan (Beitrag #64) schrieb:

Ich bleibe dabei es gibt bei der Musikaufnahme die beiden Größen : Größe Druckamplitude und zeitliche Abfolge der Änderungen.

Das ist einfach Schall und das was man wahrnimmt. ist eine Interpretation diese Schall.


Was du hören kannst und was nicht, das können Techniker und entsprechende Wissenschaftler schon spezifizieren
Was davon in deiner Innenwelt ankommt ist ein anderes Thema.

flexiJazzfan (Beitrag #64) schrieb:

Ich bleibe dabei es gibt bei der Musikaufnahme die beiden Größen : Größe Druckamplitude und zeitliche Abfolge der Änderungen. ... Die Entscheidung, was ich davon noch hören sollte und was nicht, kann meinetwegen der Tontechniker bei der Abmischung entscheiden aber nicht die Informationstechniker und Elektroingenieure deshalb : Highest Resolution !!!

Komisch, immer sollen die jenigen, die wirklich von etwas was wissen, herausgehalten werden.

Warum sind die Leute nur so wissensfeindlich?


Grüße

Unabhängig vom gespielten Ton kann man an diesen winzigen Effekten den individuellen Klang einer Trompete und die spezielle Spielweise des Trompeters (z.B. Klassik oder Jazz) erhören und erkennen.

Ja, und daran ändert eine korrekt durchgeführt A/D/A-Wandlung mit 16/44,1 überhaupt nichts.

Man kann natürlich immer noch mehr und genauere Technik fordern, aber das ist genauso, als ob man fordert, dass der Koch den Pfeffer auf dem Steak mit der Feinwaage aufs Mikrogramm genau abwiegt.
Da geht es dann irgendwann nur noch um die Gier nach technischer Perfektion und nicht mehr ums Musikhören.

Dadof3 (Beitrag #67) schrieb:

Da geht es dann irgendwann nur noch um die Gier nach technischer Perfektion und nicht mehr ums Musikhören.

Es ist eher die Unwissenheit über Technik, und eine tiefes Misstrauen gegenüber allen denjenigen, die die Technik erfunden und ermöglicht haben.
Paradox!
Ich habe ein interessantes Video gefunden, das alles erklärt:
Video

Grüße

Das Video hängt bei mir dauerverlinkt in meiner Signatur .... aber das gilt doch nur für Sinussignale, Musik ist doch unendlich komplexer (no comment)

sealpin (Beitrag #69) schrieb:

Das Video hängt bei mir dauerverlinkt in meiner Signatur .... aber das gilt doch nur für Sinussignale, Musik ist doch unendlich komplexer (no comment) :.

Und bei 24/96 sind die Zahlen doch größer als bei 16/44,1, das muss doch besser sein.

sealpin (Beitrag #69) schrieb:

Das Video hängt bei mir dauerverlinkt in meiner Signatur .... aber das gilt doch nur für Sinussignale, Musik ist doch unendlich komplexer (no comment) :.

Falls Du meinen Kommentar dazu ansprichst... Da ging es um eine Tiefe von nur 8 Bit, die Du als ausreichend bezeichnet hattest

8 Bit sind aber nur 256 mögliche Werte. Natürlich kann man damit eine Sinuskurve exakt nachbilden, aber keine komplexe Schwingung, wie sie bei Musik nunmal immer vorliegt. Die Sinuskurve ist in ihrem Verlauf vorhersehbar, komplexe Schwingungen nicht! Das ist vergleichbar mit einer Vektorgrafik und einem Foto. Bei einem Foto ist nunmal nicht vorhersehbar, wie das Pixel darüber, darunter und nebendran gefärbt sein muss, diese Information muss also gespeichert werden. Bei einem Vektor reicht die Information über den Verlauf sowie Start- und Endpunkte. Eine beliebig gross skalierbare Sinuskurve als Vektorgrafik braucht daher auch nur "ein paar" Byte Speicherplatz, ein 10-Megapixel-Foto im BMP-Format (logischerweise) 10 MB.

Und mal ganz praktisch... Die Macher der CD haben schon genau gewusst, warum sie auf 16 Bit gehen, wenn 8 Bit reichen würde, wäre das Produkt CD viel früher auf den Markt gekommen, weil es viel früher umsetzbar/bezahlbar gewesen wäre.

Ein Lesestück zur Historie der digitalen Tonaufzeichnung
http://www.aes.org/aeshc/pdf/fine_dawn-of-digital.pdf

ZeeeM (Beitrag #72) schrieb:

http://www.aes.org/aeshc/pdf/fine_dawn-of-digital.pdf

Dass mit 13-Bit gearbeitet wurde, zeigt ja, dass man versucht hat zu sparen wo man konnte. Wo man nicht konnte, wurde aber nicht gespart. Also, die Idee auf 8-Bit zu gehen, kam offenbar nie auf

Selbst MP3 und andere Komprimierungsverfahren arbeiten weiterhin mit 16-Bit, die Werte werden lediglich komprimiert gespeichert, ähnlich wie bei Flac. Und gerade diese Verfahren gehen bekanntlich in allen Bereichen an die Grenzen der Hörbarkeit (und darüber hinaus). Wenn 8-Bit also ausreichen würden, dann hätte man da wohl mit zuerst angesetzt. Bei der Samplerate geht man ja auch je nach Einstellung bis auf 32 kHz herunter...

Ich denke, wir sind einig, dass ein paarmal AD/DA Wandlung die Musik nicht hörbar verschlechtert und dass der CD Standard unserem Hörvermögen wunderbar angepasst und angemessen ist.

Wer einige unaufgeregte Kernsätze lesen will dem seien die kurzen Erklärungen von Sony empfohlen ( https://www.sony.de/...anding-digital-audio ) aus der ich hiermit zitiere:
„Da Klänge aus der realen Welt ständig variieren, stellen digitale Audioaufnahmen immer eine Annäherung an den kompletten Klangbereich aus dieser Welt dar. Fortschritte in der Aufnahmetechnologie erweitern jedoch kontinuierlich den Bereich sowie die Präzision von Klängen, die digital aufgezeichnet werden können.“
„High Resolution Audio bezieht sich typischerweise auf digitale Aufnahmen mit einer Sampling-Frequenz von 96 kHz/24 Bit oder höher. Dies liefert eine Klangqualität, die deutlich besser als die von CD- oder MP3-Aufnahmen ist – das standardmäßige CD-Audioformat hat eine Sampling-Frequenz von 44,1 kHz/16 Bit.“

Was noch 1998 diskutiert wurde findet man hier: http://www.uni-koeln.de/phil-fak/muwi/ag/tec/96.pdf

Wer wirklich tiefer eintauchen will in den aktuellen Stand der Technik und der Diskussion der kann hier sein Englisch polieren: https://people.xiph.org/~xiphmont/demo/neil-young.html
Zitat zur Bitrate: „An engineer also requires more than 16 bits during mixing and mastering. Modern work flows may involve literally thousands of effects and operations. The quantization noise and noise floor of a 16 bit sample may be undetectable during playback, but multiplying that noise by a few thousand times eventually becomes noticeable. 24 bits keeps the accumulated noise at a very low level. Once the music is ready to distribute, there's no reason to keep more than 16 bits.”
Gruß Rainer

Natürlich macht es Sinn bei der Produktion mit 24 Bit zu arbeiten, damit man genügend Abstand zum Rauschen hat, aber man macht es halt nicht um mehr Dinge/Details hörbar zu machen.

Vergleich 8Bit vs. 16Bit Audio Schipsel

Und natürlich klingt das Schice, dat rauscht wie Sau.

Tobiii2 (Beitrag #71) schrieb:

8 Bit sind aber nur 256 mögliche Werte. Natürlich kann man damit eine Sinuskurve exakt nachbilden, aber keine komplexe Schwingung, wie sie bei Musik nunmal immer vorliegt. Die Sinuskurve ist in ihrem Verlauf vorhersehbar, komplexe Schwingungen nicht!

Das ist nicht richtig. Diese Mechanismen funktionieren auch für beliebige komplexe Signale innerhalb der halben Abtastfrequenz. Da wird nichts weniger vorhersehbar, weil es stets nur genau eine Kurve gibt, die durch die im Digitalsignal vorgegebenen Punkte verläuft und nicht gegen die Bandbreitenbegrenzung verstößt. Das ist mathematisch bewiesen. Daher passt auch dein Beispiel mit der Vektorgrafik nicht, denn da gibt es kein solches mathematisches Modell.

Das einzige „Problem“ ist, dass bei der Digitalisierung durch die Reduzierung auf diskrete Werte eine Rundung der jeweiligen Amplitude erfolgt. Das gilt aber für einen Sinus genauso wie für komplexe Signale. Da kann man sich nur darüber streiten, wie genau es werden muss, damit das unhörbar wird. 8 Bit sind sicher zu wenig, 24 Bit sicher mehr als nötig. Ob 14 Bit ausreichen oder 16 oder erst 18 oder 20, drüber kann man streiten.

flexiJazzfan (Beitrag #74) schrieb:

Wer wirklich tiefer eintauchen will in den aktuellen Stand der Technik und der Diskussion der kann hier sein Englisch polieren: https://people.xiph.org/~xiphmont/demo/neil-young.html Zitat zur Bitrate: „An engineer also requires more than 16 bits during mixing and mastering. Modern work flows may involve literally thousands of effects and operations. The quantization noise and noise floor of a 16 bit sample may be undetectable during playback, but multiplying that noise by a few thousand times eventually becomes noticeable. 24 bits keeps the accumulated noise at a very low level. ..."

Ja,

aber das bezieht sich doch nur auf das "Quantisierungsrauschen".
24 Bit vollausgesteuert brächten theoretisch 144dB Rauschabstand. Es gibt aber keine AD-Wandler, die das hinbekommen. Um die 120dB sind das höchste der Gefühle. (Weil die AD-Wandler selber ein Eigenrauschen mit bringen...)

Jedes Mikrofon macht ein Eigenrauschen, das typischerweise einem Schalldruckpegel von um die 10dB bis 20dB entspricht (je nach Mikrofon und Qualität).

Um die realen 120dB Signal-Rauschabstand, die 24-Bit-AD-Wandler brächten, real zu "ernten", muss der Schalldruckpegel in den Spitzen mindestens um die 130dB betragen.

Denn der Noise-Floor des Mikrofon selber entspricht schon einem Schalldruckpegel von mindestens um die 10dB (0dB entspricht grob der Hörschwelle der Gehörs).

Wenn nun die/der SängerIn säuselt und singt statt schreit oder brüllt, so liegt der Schalldruckpegel des Gesangs so um die 80 bis 100dB in Mundnähe.
Damit hat man auf der analogen Seite vor der Wandlung "nur" einen Rauschabstand von 70 bis 90dB - 16 Bit reichen dafür völlig aus.
Ähnlich sieht es bei anderen leisen Instrumenten aus.

(Bei elektronischen Instrumenten, die den Klang digital erzeugen und auch so ausgeben, ist das natürlich anders.)

Baut man die Mikrofone wegen der Akustik nicht in unmittelbarer Mundnähe auf, steckt man die Mikros bei Blasinstrumenten nicht in die Schalltrichert, sondern im Abstand im Raum auf, sind auch die Schalldruckpegel nochmals geringer.


Den einzigen praktischen Vorteil von 24-Bit-A-D-Wandlern, den ich nachvollziehen kann, liegt in der Übersteuerungsreserve.
Damit kann man defensiv aussteuern, fängt sich niemals zusätzliches Rauschen der A-D-Wandler ein, und kann hinterher alles dynamisch-komprimiert so zusammendrücken, dass die leisesten Stellen fast so laut werden wie die lautesten.

Das ändert allerdings rein gar nichts am analogen Noise-Floor, der ja schon vor der A-D-Wandlung entsteht. Der wird bei der Dynamik-Kompression ebenfalls mit angehoben.

Grüße

sealpin (Beitrag #75) schrieb:

Natürlich macht es Sinn bei der Produktion mit 24 Bit zu arbeiten, damit man genügend Abstand zum Rauschen hat, aber man macht es halt nicht um mehr Dinge/Details hörbar zu machen.

In dem Sinne ist das völlig richtig.

Da bei der heimischen Wiedergabe seltenst Lautstärke-Pegel über 120dB gefahren werden, reichen 16 Bit da völlig aus.

Wichtig: Das Rauschen der gesamten Anlage - D-A-Wandler, Verstärker - muss leiser sein als die normalen Umgebungsgeräusche in einem Wohnzimmer, oder auch Musikzimmer, damit das Rauschen unhörbar bleibt: Dann hat man eine praktisch rauschfreie Wiedergabe.
Und jedes Wohnzimmer hat ein Grundgeräusch auch in Stille von um die 30 dB, plus minus.

Grüße

Dadof3 (Beitrag #77) schrieb:

Daher passt auch dein Beispiel mit der Vektorgrafik nicht, denn da gibt es kein solches mathematisches Modell.

Der Wandler berechnet also keinen sinusförmigen Verlauf (Kurve) zwischen zwei Werten?

Dadof3 (Beitrag #77) schrieb:

Das einzige „Problem“ ist, dass bei der Digitalisierung durch die Reduzierung auf diskrete Werte eine Rundung der jeweiligen Amplitude erfolgt.

Das Rundung zu nennen, klingt aber verharmlosend. Es gibt nur 256 mögliche Werte bei 8-Bit.

Bei 4-Bit sind es 16 Werte, bei 1-Bit nur zwei Werte (quasi laut oder leise). So sieht dann auch der Spannungsverlauf aus:
https://de.wikipedia...ia/Datei:Amplqrp.png

Edit: Ich habe vor Jahren mal ein Seminar besucht (Physiker, VHS), da wurde ein Musikbeispiel mit 4-Bit vorgeführt, das war nur "Schrott" und kaum erkennbar. Ein Sinuston bei 4-Bit klang wie der 16-Bit Sinuston, von Nebengeräuschen/Rauschen mal abgesehen. Erklärung dafür wie von mir hier wiedergegeben.

Man sieht hier ganz gut was passiert:

Nee, so sieht der nicht aus. Da sind ja wieder Treppenstufen abgebildet - die gibt es nicht!

Der Wandler "berechnet" den Verlauf nicht, jedenfals nicht im herkömmlichen Sinne, aber er rekonstruiert ihn. Und er muss nicht (rein) sinusförmig sein, sondern es ist eine Überlagerung beliebiger Sinuswellen innerhalb der Bandbreite.

Ich weiß, das ist schwer vorstellbar - ich habe damit auch anfangs schwer getan, dass das so gehen soll. Es entspricht nicht unbedingt dem gesunden Menschenverstand.

Dadof3 (Beitrag #81) schrieb:

Nee, so sieht der nicht aus. Da sind ja wieder Treppenstufen abgebildet - die gibt es nicht!

Die gibt es im Analogsignal nicht, weil der Wandler eine Kurve rechnet, ja. Der Wandler nimmt immer einen sinusförmigen Verlauf an, deshalb passt das bei einem Sinuston ja auch perfekt. Aber darum geht es doch nicht, die Rechteckdarstellung wurde da (wird meistens) gewählt, um das Problem deutlich zu machen, nämlich dass es nur zwei Werte gibt, die bei einer 1-Bit-Wandlung möglich sind, laut oder leise. Bei 4-Bit gibt es 14 weitere Abstufungen. Deshalb rauscht es bei 1-Bit doch so extrem, das Rauschen bekommt den gleichen Wert (laut) zugewiesen wie der Ton (laut).

Das Rechtecksignal zeigt nur die Endlichkeit einer Fourierreihe.
Auch berechnet der Wandler selber nix, das mach analog wie auch digital ein Tiefpass,
Die noch direkt nach dem Wandler enthalten Treppchen enthalten höherfrequente Terme der Reihe, schneidet man die ab, dann wird der Sinus rund und die Kanten eines Rechtecks sehen aus, wie sie nach so einem Vorgang aussehen.
Auch Musik, die bei der AD Wandlung einen Tiefpassfilter durchlaufen hat enthält nix, was man nicht so rekonstruieren könnte

Tobiii2 (Beitrag #82) schrieb:

Dadof3 (Beitrag #81) schrieb: Nee, so sieht der nicht aus. Da sind ja wieder Treppenstufen abgebildet - die gibt es nicht! Die gibt es im Analogsignal nicht, weil der Wandler eine Kurve rechnet, ja. Der Wandler nimmt immer einen sinusförmigen Verlauf an,

Falsch.
Der Wandler nimmt an, dass es sich bei dem Digital-Signal, was er auf analog wandeln soll, um ein gemäß dem Abtast-Theorem bandbreiten-begrenztes Signal handelt. Ob sinus-förmig oder nicht, ist dabei egal.

... nämlich dass es nur zwei Werte gibt, die bei einer 1-Bit-Wandlung möglich sind, laut oder leise. Bei 4-Bit gibt es 14 weitere Abstufungen. Deshalb rauscht es bei 1-Bit doch so extrem,

Das stimmt.

das Rauschen bekommt den gleichen Wert (laut) zugewiesen wie der Ton (laut).

Das ist zumindest missverständlich.

Grüße

Burkie (Beitrag #84) schrieb:

Der Wandler nimmt an, dass es sich bei dem Digital-Signal, was er auf analog wandeln soll, um ein gemäß dem Abtast-Theorem bandbreiten-begrenztes Signal handelt. Ob sinus-förmig oder nicht, ist dabei egal.

Ich habe leider schon lebenslang eine starke Motivationslosigkeit mich mit Mathematik zu beschäftigen, insb. wenn sie mir keinen praktischen Nutzen bietet, daher verzeih ' mir die Rückfrage(n)

Abgetastet wird mit doppelter Frequenz der höchsten Frequenz die gespeichert werden soll. D.h., bei 48 kHz erfolgt die Abtastung bei 24 kHz also "jede halbe Schwingung" (mal auf einen Sinus bezogen). Das ist ja nun nicht so genau, dass man ohne irgendeine mathematische Funktion den Kurvenverlauf rekonstruieren kann. In wikipedia steht die Rekonstruktion geschieht mittels "Polynominterpolation". Und wenn ich das richtig verstehe, ist eben das die Funktion, welche die Zwischenwerte und damit den Kurvenverlauf berechnet? Und diese Funktion muss doch irgendeine Vorgabe bekommen, wie der Verlauf zwischen den Werten berechnet werden soll, könnte ja auch einfach eine Gerade sein?

Tobiii2 (Beitrag #85) schrieb:

Burkie (Beitrag #84) schrieb: Der Wandler nimmt an, dass es sich bei dem Digital-Signal, was er auf analog wandeln soll, um ein gemäß dem Abtast-Theorem bandbreiten-begrenztes Signal handelt. Ob sinus-förmig oder nicht, ist dabei egal. Ich habe leider schon lebenslang eine starke Motivationslosigkeit mich mit Mathematik zu beschäftigen,

Hallo.

Dann sind weitere Erklärungen auf dieser Ebene sinnlos.

Wenn du kein Interesse an den Erklärungen hast, ist es sinnlos, es dir zu erklären.

Hör es dir einfach an, und fertig.

Und wenn dir dann immer noch sog. "Hi-Resolution"-Aufnahmen besser klingen, dann sei es so für Dich rein persönlich.

Grüße

Burkie (Beitrag #86) schrieb:

Wenn du kein Interesse an den Erklärungen hast, ist es sinnlos, es dir zu erklären.

Wenn es mich nicht interessieren würde, hätte ich nicht gefragt... Ich wollte damit nur sagen, dass mir die Grundlagen fehlen, die "Lagrangesche Interpolationsformel" zu verstehen. Ich bezweifle aber auch, dass Du sie verstehst.

Burkie (Beitrag #86) schrieb:

Und wenn dir dann immer noch sog. "Hi-Resolution"-Aufnahmen besser klingen, dann sei es so für Dich rein persönlich.

Bitte? Eben verwechselst Du mich aber...

Tobiii2 (Beitrag #87) schrieb:

Burkie (Beitrag #86) schrieb: Wenn du kein Interesse an den Erklärungen hast, ist es sinnlos, es dir zu erklären. Wenn es mich nicht interessieren würde, hätte ich nicht gefragt... Ich wollte damit nur sagen, dass mir die Grundlagen fehlen,

Eben.

Schau dir dies Video an:
https://www.youtube.com/watch?v=cIQ9IXSUzuM

Das sind die Grundlagen.

Grüße

Burkie (Beitrag #88) schrieb:

Eben. Schau dir dies Video an: ...

Das hat er doch längst getan. Da wird auch nicht alles beantwortet.

Tobiii2 (Beitrag #87) schrieb:

Wenn es mich nicht interessieren würde, hätte ich nicht gefragt... Ich wollte damit nur sagen, dass mir die Grundlagen fehlen, die "Lagrangesche Interpolationsformel" zu verstehen. Ich bezweifle aber auch, dass Du sie verstehst.

Ich verstehe sie auch nicht, bzw. ich habe es auch gar nicht versucht. Ich habe auch den Beweis für das Nyquist-Shannon-Abtasttheorem nicht studiert. Mir reicht es, dass die Wissenschaft es für bewiesen hält.

Ich habe aber immerhin im Studium gelernt, wie das mit den Fouriertransformationen funktioniert. Berechnen kann ich da auch nichts mehr, zu lange her, aber das Grundprinzip ist haften geblieben. Das hilft sicher beim Verständnis. Der Grundgedanke ist, dass jede Schwingung, so komplex sie auch sein mag, eine Überlagerung von reinen Sinuswellen diverser Amplituden und Frequenzen darstellt. Für manche Signale muss man dann sehr hohe Frequenzen bemühen. Diese können wir aber nach aller wissenschaftlicher Erkenntnis nicht hören. Deswegen macht es nichts, wenn diese nach der Wandlung fehlen. Man begrenzt also die Bandbreite der möglichen Lösungen künstlich, und das hat dann zum Ergebnis, dass es dafür dann bei ausreichender Abtastrate von 2 x fmax nur jeweils eine mögliche Lösung gibt. Diese ist nicht exakt das ursprüngliche Signal! Aber die Abweichung gilt als nicht hörbar, weil das Trommelfell dem einfach nicht mehr folgen kann.

Das ist ja nun nicht so genau, dass man ohne irgendeine mathematische Funktion den Kurvenverlauf rekonstruieren kann. In wikipedia steht die Rekonstruktion geschieht mittels "Polynominterpolation". Und wenn ich das richtig verstehe, ist eben das die Funktion, welche die Zwischenwerte und damit den Kurvenverlauf berechnet? Und diese Funktion muss doch irgendeine Vorgabe bekommen, wie der Verlauf zwischen den Werten berechnet werden soll, könnte ja auch einfach eine Gerade sein?

Die könnte man jetzt auch per "Polynominterpolation" berechnen, aber faktisch bekommt man das auch ganz ohne Arithmetik mit einem einfachen Tiefpassfilter hin, der alle Frequenzen über fmax herausfiltert. Eine Gerade würde je nach Steilheit entweder genügend Stützpunkte haben, um hinreichend eindeutig rekosntruiert zu werden, oder sie enthält Frequenzanteile, die nicht mehr innerhalb der Bandbreite liegen.

Tobiii2 (Beitrag #85) schrieb:

Das ist ja nun nicht so genau, dass man ohne irgendeine mathematische Funktion den Kurvenverlauf rekonstruieren kann.

Je nachdem, wie man "Mathematische Funktion" betrachtet. Ein Tiefpassfilter ist in gewisser Weise auch eine mathematische Funktion.

Dadof3 (Beitrag #89) schrieb:

Burkie (Beitrag #88) schrieb: Eben. Schau dir dies Video an: ... Das hat er doch längst getan. Da wird auch nicht alles beantwortet.

Die Grundlagen schon.

Wenn er aber eine Abneigung gegen Mathematik, ein tiefes Misstrauen gegen Wissenschaft hat, ist alles reden sinnlos.
Er wird uns, ohne etwas davon zu verstehen, stets zu beweisen versuchen, dass Mathematik, Wissenschaften und Abtastheorem "falsch" sind.


Geben wir uns doch einfach geschlagen und ihm in allen Punkten recht!
Er ist eben mit seinem "gesunden Menschenverstand" schlauer als alle Wissenschaftler, Mathematiker und Ingenieure zusammen.
Musik ist eben so "komplex", die widersetzt eben jeder Signaltheorie oder jeder Technik.


Grüße

Burkie (Beitrag #90) schrieb:

ein tiefes Misstrauen gegen Wissenschaft ... Er wird uns, ohne etwas davon zu verstehen, stets zu beweisen versuchen, ...

Ich habe keine Ahnung, wie du zu solchen Annahmen und Schlussfolgerungen kommst. Ich sehe da eher ein Bedrüfnis, das ganz auch ohne Mathemtaikkenntnisse verstehen zu wollen.

Und ich habe das Bedürfnis, ganz auch ohne Physik den Urknall zu verstehen.

Grüße

Dafür lassen wir ja tausende von Euros bei Hifi Händlern, in der Hoffnung das Elekronik und Physik harmonieren...

Dadof3 (Beitrag #91) schrieb:

Ich habe keine Ahnung, wie du zu solchen Annahmen und Schlussfolgerungen kommst. Ich sehe da eher ein Bedrüfnis, das ganz auch ohne Mathemtaikkenntnisse verstehen zu wollen.

Danke, ich habe auch keine Idee wie er zu einer solchen Schlussfolgerung kommt. Ich würde keine "Physik-Vorlesungen" besuchen, wenn es so wäre.

Um meine Frage von oben nochmal vorzubringen: Nehmen wir als Beispiel für eine Abtastung also einen 24 kHz Sinuston, den wir mit 48 kHz abtasten. Gemäss Theorem ist der so vollständig rekonstruierbar:


Die roten Linien zeigen die Abtastpunkte, bei 24 kHz also bei 0° und 180°. Das kann kaum ausreichen für eine Rekonstruktion, weil so nicht einmal die Amplitude erfasst würde.

Also muss die Abstastung um 90° versetzt erfolgen:


So würde es gehen. Aber eben auch nur, wenn die Rekonstruktionsfunktion wirklich einen sinusförmigen Verlauf annimmt. Was wir da auch sehen, eine Tiefe von 1 Bit würde hier ausreichen, um die Amplitude zu speichern, weshalb 8 Bit wie im von "sealpin" verlinkten Video mehr als ausreichen. Das bedeutet aber nicht, dass jede noch so komplexe Schwingung mit 8-Bit erfasst exakt rekonstruiert werden kann, weil 256 mögliche Werte einfach viel zu ungenau abbilden würden, schon bei solchen Schwingungen: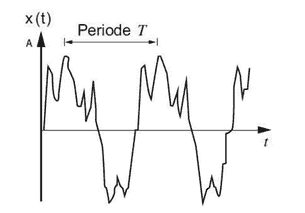


Das ist lediglich ein immer noch sehr simpler Sinus mit Obertönen und kleinen Störungen, der Verlauf ist daher natürlich nur noch sinusähnlich. Wenn man den rekonstruiert und eine Sinuskurve aus den Zwischenwerten rechnet, kommt wieder ein sauberer Sinus heraus. Und Alles was über 24 kHz lag, wie die Obertöne, ist weg. Da ist er also, der Tiefpass...

Nehmen wir noch einen Sinus bei 750 Hz:


Der wird etwa alle 6° abgetastet, weshalb die Rekonstruktion natürlich viel exakter erfolgen kann. Ich denke das erklärt auch gut, weshalb es im Grenzbereich der Nutzbandbreite zu Fehlern und Verzerrungen kommt. Die Abtastrate auf 96 kHz zu erhöhen, würde die Fehler nicht nur in ganz andere Frequenzbereiche bringen, auch die Abtastung wäre durchaus exakter. Mal das obige Beispiel mit einer Abtastrate von 192 kHz:


Ich denke daher auch, dass man da durchaus von höherer Auflösung sprechen kann. Was davon hörbar wird, ist natürlich eine ganz andere Frage. Aber... Ich höre nur noch etwa 15 kHz, theoretisch würde also eine Abtastrate von 32 kHz mehr als ausreichen. Allerdings höre ich Unterschiede, wenn ich ein Lied entsprechend konvertiere (was ja nun nicht an der fehlenden Bandbreite liegen kann)...

Da muss nix berechnen, keine angenommenen Kurvenverläufe nix
Einfach durch ein steilflankiges Tiefpassfilter und das digitalisierte Signal ist da.
Man darf sich vergessen das auch bei der Aufnahme ein Tiefpassfilter am werkeln ist.
Diese Filter kann man auch auf der digitalen Ebene rechnen. Aber unter Shannon Nyquist Bedingungen arbeitet und das tut man in der Praxis, dann muss zwischen den Abtastpunkten nix geraten werden.
Das Rechteck das man vor der AD Wandlung durch den Tiefpass schickt, ist dahinter kein Rechteck mehr.
Das ist auch wurscht, es sei denn man ist Superohr das ein 20Khz Rechteck von ein 20KHz Sinus hörbar unterscheiden kann.

ZeeeM (Beitrag #95) schrieb:

Da muss nix berechnen, keine angenommenen Kurvenverläufe nix Einfach durch ein steilflankiges Tiefpassfilter und das digitalisierte Signal ist da. :)

So ein Tiefpassfilter ist etwas tolles, noch toller, wenn man es wie Du einfach als gegeben ansieht und nicht versucht zu verstehen, wie es intern arbeitet

Ich habe es doch dargelegt, wenn man aus zwei Messpunkten einen sinusförmigen Verlauf zwischen diesen berechnet, ist Alles was über der halben Abtastfrequenz liegt, weg. Mit entsprechenden Ungenauigkeiten. Das ist der Tiefpass.

Aber es reicht auch fast schon, zu wissen, was Interpolation bedeutet, nämlich "Zwischenwerte berechnen" exakter: "Werte zwischen bekannten Werten einer Funktion errechnen".

Tobiii2 (Beitrag #94) schrieb:

Um meine Frage von oben nochmal vorzubringen: Nehmen wir als Beispiel für eine Abtastung also einen 24 kHz Sinuston, den wir mit 48 kHz abtasten. Gemäss Theorem ist der so vollständig rekonstruierbar: Die roten Linien zeigen die Abtastpunkte, bei 24 kHz also bei 0° und 180°. Das kann kaum ausreichen für eine Rekonstruktion, weil so nicht einmal die Amplitude erfasst würde. Also muss die Abstastung um 90° versetzt erfolgen:

Du hast das Nyquist-Shannon Theorem offenbar nicht in allen Details verstanden. Ich wiederhole mal das wichtigste:

...unterhalb der Nyquist-Frequenz...

Na, klickert's?

Mikesch_75 (Beitrag #97) schrieb:

Na, klickert's?

Nö

Ist doch die halbe Abtastfrequenz. 24 kHz Sinuston, Abtastung mit 48 kHz, also zwei Messpunkte pro Sinus. Wenn die Messpunkte an den Nulldurchgängen liegen, kann die Amplitude nicht erfasst werden. Das hatte ich versucht mit den beiden von Dir zitierten Grafiken darzustellen.

Was ist falsch daran?

Was ist falsch daran?

Wie Mikesch_75 auch schon oben geschrieben hat ist die Nyquist Bedingung keine Gleichung, sondern eine Ungleichung, nämlich ein bandbegrenztes Signal kann aus einer Folge von äquidistanten Abtastwerten exakt rekonstruiert werden kann, wenn es mit einer Frequenz von größer als 2 * fmax abgetastet wurde.

Die höchste zu übertragende Frequenz muss demnach kleiner sein als die halbe Abtastfrequenz, sonst entstehen Aliasingfehler. Aus diesem Grund werden höhere Frequenzen aus dem analogen Signal mit einem Tiefpass herausgefiltert. Die Aliasingfehler sind Alias-Signale (Störsignale, Pseudosignale), die sich bei der Rekonstruktion als störende Frequenzanteile bemerkbar machen. Wird zum Beispiel ein Sinussignal, das eine Frequenz von 1600 Hz hat, mit einer Abtastfrequenz von 2000 Hz digitalisiert, erhält man ein 400-Hz-Alias-Signal (2000–1600 Hz). Bei einer Abtastfrequenz über 3200 Hz entsteht dagegen kein Alias-Signal. Eine Abtastfrequenz von bspw. 3300 Hz führt zu einem Differenzsignal von 1700 Hz (3300–1600 Hz). Dieses ist jedoch größer als die halbe Abtastrate und wird demnach bei der Rekonstruktion durch einen Tiefpass entfernt.

In der Praxis gibt es keinen idealen Tiefpass. Er hat immer einen gewissen Übergangsbereich zwischen praktisch keiner Dämpfung im Durchlassbereich und praktisch vollständiger Dämpfung im Sperrbereich. Daher verwendet man in der Praxis eine modifizierte Formel zur Bestimmung der Abtastfrequenz:

Beispiel: fabtast = 2,2 * fmax

Auf einer CD wird ein Signal gespeichert, das durch die Digitalisierung eines analogen Audiosignals mit Frequenzen bis 20 kHz erzeugt wird. Die Frequenz, mit der das analoge Audiosignal abgetastet wird, beträgt 44,1 kHz.

Der verwendete Faktor ist abhängig vom verwendeten Tiefpassfilter und von der benötigten Dämpfung der Alias-Signale. Andere gebräuchliche Faktoren sind 2,4 (DAT, DVD) und 2,56 (FFT-Analysatoren)

Kann man auch alles in Wikipedia lesen https://de.wikipedia.org/wiki/Nyquist-Shannon-Abtasttheorem

thewas (Beitrag #99) schrieb:

Was ist falsch daran? Eine Abtastfrequenz von bspw. 3300 Hz führt zu einem Differenzsignal von 1700 Hz (3300–1600 Hz).

Eine Abtastung mit 48000 Hz ergibt dann bei einem 24000 Hz Sinus ein Differenzsignal von 0 Hz. Aber gut, dann nehmt doch einfach an, das Signal in meiner Grafik wäre ein 23,9 kHz Sinus.